10 FUN MATHEMATICAL FACTS
Mathematics sucks. Mathematics is hard and it is useless…
Here are the sentences we can hear every day about mathematics, a discipline that is so important! And so much fun if you take the time to take a closer look…
In La Maison de Fermat in the South of France, and in many math spaces like this one, we are trying to change the way young (and not so young) people look at mathematics. We are developing another idea of math… and that vision is much more fun!
Here is the proof with 10 amazing facts seen with another look at mathematics!
1. My friend Cédric Villani
For mathematicians, social networks can be represented by giant graphs (a graph is a diagram containing points called vertices, connected or not by segments called edges or links). There can be hundreds of millions of vertices (profiles) and links (friends).
Many mathematicians have been interested in the density of exchanges, the popularity or not of certain accounts… They have seen that all social networks work in the same way. A majority of people have few (friends) links and a minority has many. Moreover, and this seems logical, two people who have a common friend will have a better chance of becoming friends in turn. That’s why your favorite social network often suggests friends of friends. All this is calculated….
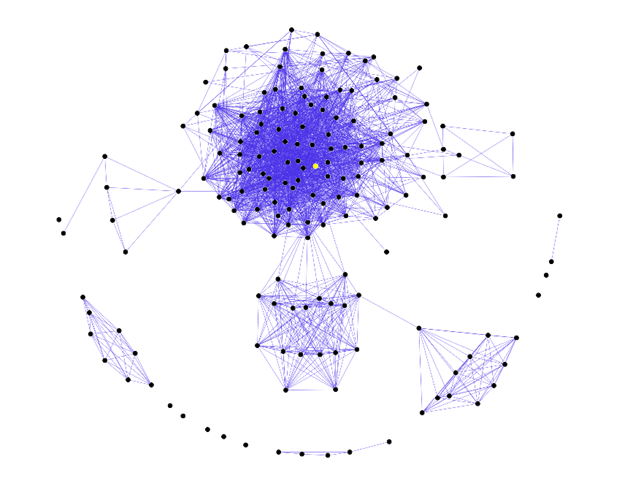
A fictional social network diagram.
It consists of 165 vertices and 1851 edges.
[Source https://en.wikipedia.org/]
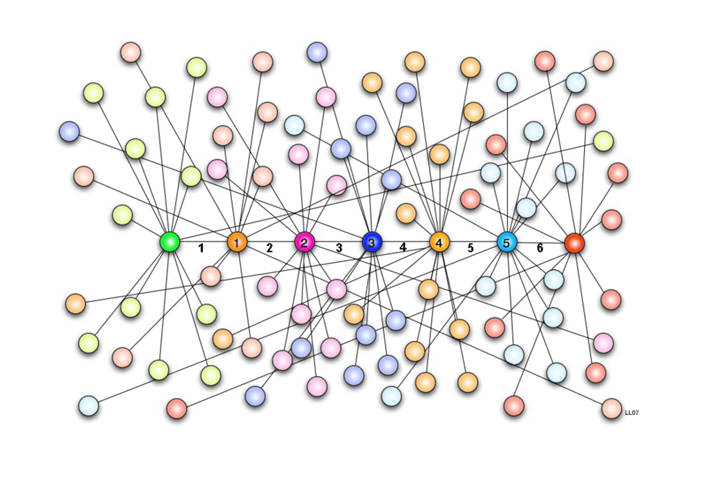
Artistic visualization of the Six Degrees of Separation principle [Source https://fr.wikipedia.org/]
Another theory related to networks is the theory of six degrees of separation, established by the Hungarian Frigyes Karinthy in 1929, which evokes the possibility that any person on Earth can be connected to any other person, through a chain of individual relationships comprising at most five other people.
With the development of social networks, this degree of separation was measured at 4.74 on Facebook in 2011 and around 3.5 degrees in 2016. The latest study was conducted following the exchange of several billion instant messages studied in 2008 by Eric Horvitz and Jure Leskovec, researchers at Microsoft.
This theory is most effectively used on the LinkedIn professional network which reports the degree of separation between two individuals as well as the possible “paths” that connect one individual to another through their respective relational networks
2. Holy π !
Pi, sometimes called Archimedes’ constant, is a number represented by the lower-case Greek letter of the same name: π. The use of this Greek letter π, the first letter of περίμετρος (“perimeter” in ancient Greek), did not appear until the 18th century. Previously, its value was referred to by various periphrases as the “constant of the circle” or its equivalent in various languages.
This constant is found in everything that is round or animated by a circular movement. It’s up to you to check it out! Take any round object, such as a plate or bicycle wheel, measure its circumference and then its diameter. Divide the circumference by its diameter, you will get a little more than 3, and more precisely π.
3. Gauss and mental calculation

Nicknamed the Prince of Mathematicians, Carl Friedrich Gauss studied all fields of mathematics and contributed to the development of most branches of science.
A child prodigy, it is said that he was able to read and count from the age of three and it is also said that he demonstrated a remarkable talent for mental calculation. On a school day, his teacher asked him to calculate the sum of the numbers from 1 to 100. After a very short time, the then 10-year-old Gauss gave the answer to this complex operation using a technique that consisted in grouping the extreme terms in pairs. Without knowing it yet, Gauss had discovered the formula for calculating the sum of the terms of an arithmetic sequence.
He did :
(1 + 100)
+ (2 + 99)
+ (3 + 98)
+ …
+ (50 + 51)
= 101 x 50 = 5 050
4. Simpson and Fermat
In one of the Simpsons’ episodes, we can see an equality that will recall a famous theorem of the mathematician Pierre Fermat:

178212 + 184112 = 192212
In mathematics, and more precisely in number theory, the last Fermat theorem, or great Fermat theorem, or since its demonstration Fermat-Wiles theorem, is stated as follows:
There are no strictly positive integers x, y and z such that x n + y n = z n as soon as n is an integer strictly greater than 2.
Would Homer have demonstrated otherwise?
Of course not! But, strangely enough, if we try to prove this equality with our calculator we see that it is correct… What happens then?
Quite simply the numbers are so large that the calculator will round them off… Indeed, these two numbers (the sum of (178212 + 184112) then 192212) have their first eight identical digits but are not equal!
5. GOOGLE
Some numbers are so large that we have difficulty imagining them. Googol for example is a number equal to 1 followed by 100 zeros (or 10100). The word googol is first mentioned by the American mathematician Edward Kasner in his book Mathematics and the Imagination published in 1938. Kasner is said to have asked his nephew, then 9 years old, to baptize the number he had just created. He would have simply replied: “Googol“.
Gogol is explicitly claimed by Google’s founders as a model for their company’s name: “Google chose this term to symbolize its mission: to organize the immense volume of information available on the Web. ».

6. Birthday Paradox
If you put 23 people in a room, there is a 50% chance that 2 of them share the same birthday… The birthday paradox results from the probabilistic estimate of the number of people that must be gathered to have at least a one in two chance that two people in this group have their birthday on the same day. It so happens that this number is 23, which shocks the intuition a little. From a group of 57 people, the probability is greater than 99%.
This is a paradox not in the sense of a logical contradiction, but in the sense that it is a mathematical truth that contradicts intuition: most people believe that this probability is much lower than 50%. This study is by Richard von Mises.
7. Pringles and maths

The particular shape of these chips has been designed from a supercomputer. Especially to keep the chips from flying… From flying?
Indeed, during their manufacture, the chips used a conveyor belt. To increase production, the speed of this conveyor had to be increased and the chips started to fly away. So engineers looked into the issue, and using a supercomputer, a form of hyperbolic paraboloid was developed to solve the problem.
8. Long live Kings and Queens
How likely is it to find the bean when cutting a cake of kings? Mathematicians have tried to clarify this question!
For this probability calculation, the following hypotheses were considered: guests (8 precisely) equally share a 25 cm diameter cake with a circular bean 2.5 cm in diameter. It should also be remembered that the position of the bean has a very strong influence on the probability of finding it when the cake is cut. Indeed, if the bean is in the center of the cake, the person who cuts it is sure to find it.
After a careful calculation, and taking into account these hypotheses, it has been demonstrated that there is at least a 1 in 4 chance of finding the bean by cutting the cake for these dimensions.
That’s why we come across it so often!

9. Get into the round!
Whether there are 10, 100 or 1000 of us in a round, everyone has to move back 28 cm to add a person to a circle… Really?
Instinctively, there is a tendency to believe that adding a person to a circle of 1000 people will only make each person move back a few millimetres so that they have their place in the circle. However, this is not the case because the perimeter and radius of the circle are proportional: P = 2 * π * R
So if we change the perimeter by 1.75 m (which is approximately the size of a man), we must change the radius by 1.75/(2 * π) or approximately 0.28m so that the circle remains homogeneous.
10. A question of form....

It is no coincidence that the manhole covers are round. This choice is linked to security reasons.
By giving it this shape and a slightly larger diameter than the hole, its designers have ensured that it cannot physically fall into the hole.
A square, rectangular or triangular plate could not have offered the same guarantees, as it could have fallen into the hole by its diagonal.
Find all this information and more in the articles below (in French):
- https://fr.spontex.org/le_saviez_vous/
- http://www.motivationfactory.com/blog/innovation/belle-histoire-pringles
- https://www.cnews.fr/racines/2014-09-02/pourquoi-les-plaques-degout-sont-elles-de-forme-ronde-690604
- https://www.wellcom.fr/wnews/2011/12/la-fin-du-six-degres-de-separation/]
- https://www.maths-et-tiques.fr/
- https://www.babelio.com/livres/Louart-Cest-mathematique-/616675
- http://www.topito.com/top-fun-fact-mathematiques-cool
