Non-formal approach to teaching mathematics
In recent years, the issue of mathematical skills has become increasingly important. They are classified as key competences necessary for personal fulfilment, active citizenship, social inclusion and employability in a knowledge-based society.
Children’s first experiences are crucial, but students too often fear mathematics and some change their schooling to avoid them. Different approaches can improve attitudes, restore the taste for discovery, so raise the levels achieved and open up new learning opportunities to satisfy children’s need to learn.
We have seen in recent years a movement in the way of teaching mathematics: a non-formal approach to learning mathematics with more research activities and less computational exercises.
The approaches and methods used to discover mathematics can have a significant impact on how students learn in the classroom, as well as on the quality of their learning. If appropriate, they can improve students’ level of understanding and help them master mathematical rules and procedures. The methods used also influence the enjoyment that students take of learning, which in turn has an indirect impact on what they learn, both in quantitative and qualitative terms.
Definitions of the terms
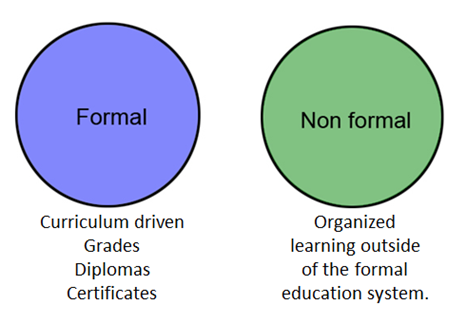
Formal education and non-formal education are two ways of looking at education. Let us first define these two approaches:
Formal learning is that which is provided in an organised and structured context (e. g. in an educational or training institution, or in the workplace), and is explicitly designated as learning (in terms of objectives, time or resources).
Non-formal learning is integrated into planned activities that are not explicitly designated as learning activities (in terms of objectives, time or resources), but which include an important learning element.
Organizational learning, source : .imranchohan.com
Non formal education and playful mathematics
Making math fun does not mean making it simpler and even less lowering the level. It is even surprising to see how complex notions can be conveyed through play.
Fun mathematics replaces obligation with instruction. The student is not obliged to do anything except follow a game instruction. He quickly realizes that a good understanding of the instructions allows him to succeed in the manipulation undertaken, as Stella Baruk, professor of mathematics and researcher in psychology, points out in her books on education.
It is then a question of the student placed in a playful learning situation to understand and not to apply rules imposed on him. This way of de-dramatizing mathematical learning makes it possible, once confidence is restored, to return painlessly to more formal teaching.
The notion of game is very broad, it can go from a traditional game with two or more players (Hex game), to a magic trick to understand, through origami, enigmas or the construction of strange objects (like hexaflexagons for example). Playing a game is a good way to approach a mathematical notion.

Jeu de Hex, source : images.math.cnrs.fr

Hexaflexagon, source : JustOrigami
An example of a fun workshop: the Tangram
Tangram can be used to develop children’s observational skills and introduce them to geometry in an empirical and visual way.
The origins of this game go back to the 16th century in China: a legend tells us that an emperor, admiring a magnificent faience tile, inadvertently dropped it on the ground, where it broke into seven pieces. Trying to reconstruct the broken tile, he was never able to do so and recreated thousands of different figures instead. The Tangram game was recently imported into the West: the first known works describing it date back to the end of the 18th century.
The rule is simple: after having followed a construction program to create his Tangram pieces, the instruction is to make silhouettes representing characters, geometric figures, animals, letters… All the pieces must be used and they can only be juxtaposed and not superposed. There are a very large number of possibilities, there are about 2000 geometric or figurative models, more or less complicated.
Another playful approach: the history of mathematics
The history of mathematics makes it possible to understand certain mathematical concepts by placing them in their context. This approach makes it possible to give meaning to learning that, in the eyes of the students, ran the risk of being deprived of it. Instead of notions detached from life, it has the merit of restoring mathematics in the evolution of humanity, in culture. Using math history can also become a good way to create motivation by telling mathematical discoveries as part of the human adventure. This makes it possible to give the discoverer the desire to better understand, for example, with Thales and the measurement of the pyramid, Eratosthenes and the measurement of the circumference of the Earth or the extraordinary story of Pierre Fermat’s Great Theorem.

Eratosthenes research, source : gerard-verhoest.com
Conclusive results
The level of motivation to learn mathematics is an important determinant of students’ academic performance. National strategies to increase student motivation are in place in almost half of European countries.
Improvement is not necessarily immediate, but when confidence is restored and tools are given to understand and succeed, the student’s state of mind in relation to mathematics is changed.
According to Stella Baruk, children can be passionate about this subject as early as first grade. Mathematics is useful and necessary in more and more fields, in computer science of course but also in the whole economy: statistics, geometry, probability, etc… Promoting the scientific approach through appropriate means means means promoting creativity and innovation, thus revitalizing education and the economic fabric
Mathematics careers, source : tun.com

